Algorithme
et technologie
Les différents
programmes disponibles sur ce site proposent plusieurs solutions au problème
classique du cavalier d'Euler. Ce problème est abordé sous deux aspects.
L' algorithme
Comment concevoir l'algorithme pour que la recherche soit la plus
rapide possible ? Comment prendre en compte dans l'algorithme les contraintes
nécessaires à l'élaboration d'un carré magique
et quels sont tous les carrés magiques
possibles ?
Les technologies
informatiques
Comment intégrer simplement le programme de recherche dans un environnement Web pour le rendre directement utilisable à travers une page HTML ?
En 2004, il
fallait plus de 50 jours pour trouver toutes les solutions de carrés magiques.
En 2011, les 140 solutions sont trouvées en moins de 4 jours. Le temps de
recherche a été divisé par 15 en 7 ans. En 2017, il suffit de 1,3 jour. Cette
réduction est due à la fois à des améliorations dans l'algorithme de recherche
et à l'utilisation de processeurs plus performants (pentium 4 2,4 Ghz en 2004,
i3 2330 en 2011, i5 4310M en 2016, i72600 en 2017. En 2019 les solutions sont trouvées en 0,7 jour sur un AMD Ryzen 5 1600X - 3.6GHz..
L'algorithme de
recherche est basé sur 64 objets coopérants, représentant les 64 cases de
l'échiquier. La présentation suivante 
décrit les principales fonctions de recherche
. L'algorithme est
implémenté sous forme d'un contrôle ActiveX (Kmagic.ocx) qui peut être intégré dans une présentation. Les paramètres de supervision de
l'algorithme sont présentés dans un autre contrôle activeX, mschrt20.ocx qu'il faut également enregistrer.
Les résultats,
après parallèlisation de l'algorithme sur plusieurs threads indépendants, sont
synthétisés dans le tableau suivant.
:
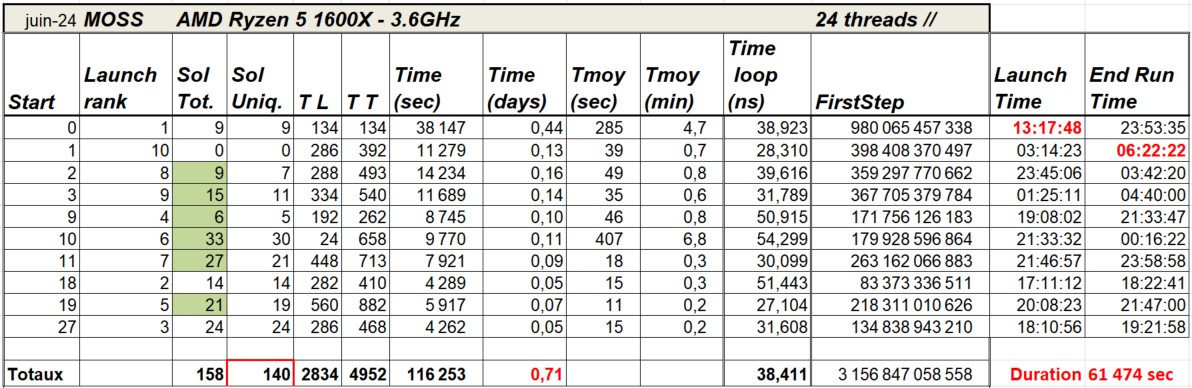
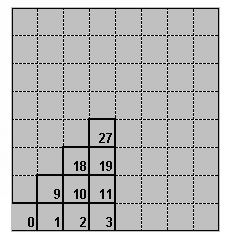
Start : indique le numéro de la case de départ pour la recherche. Les 10
départs correspondent aux cases numérotées 0,1,2,3,9,10,11,18,19,27.
rang : l'ordre dans lequel les 10 recherches (à partir des 10 départs)
sont lancées. Ces recherches sont lancées en séquence, les unes après les
autres. Une améliroation récente consiste à ne pas attendre la fin d'une séqunce pour lancer la recherche suivante à partir d'un nouveau départ. Pour chaque nouvelle recherche, on supprime de la liste des fins de
parcours possible les cases, et toutes leurs symétries sur l'échiquier, qui ont
déjà été utilisées comme case de départ d'une recherche précédente. Cette méthode
permet de réduire le temps de recherche en évitant de trouver 2 fois les
solutions (1 chemin direct et un chemin retour)
Sol. Tot. :le nombre total de solutions trouvées. Certaines solutions
trouvées ont des relations de symétrie, comme c'est le cas pour les 2 solutions
de l'exemple suivant. La case de départ est la case 3.
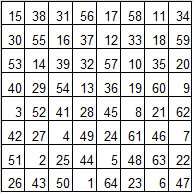
Le chemin inverse
de la première solution (chaque valeur x est remplacée par 65 - x) donne la
solution suivante.
qui est une
symétrie de la seconde solution.
Sol. uniq. : nombre de solutions indépendantes, une fois que toutes les
symétries ont été supprimées
Temps (sec) : temps en secondes de la recherche complète à partir de la case de
départ
Temps (jours) : temps en jour (secondes/86400)
Temps loop (ns) : temps / Firstep en nanosecconds
FirstStep :nombre de bonds en avant du cavalier pour parcourir l'ensemble de
l'arbre de recherche
il y a 280 tours magiques avec différentes propriétés: standard, chemins fermés, chemins semi-magiques où chaque quart de l'échiquier est lui même un carré magique. Chaque tour est lié a un autre tour qui est son chemin inverse qui est également magique. Par conséquent, il n'y a que 140 tour magiques.
Chemin fermé
Un chemin fermé (CT) est un chemin où la première case (index 1) et la dernière (index 64) sont en relation par un bon du cavalier.
2KT Tours
D'autres types de tour peuvent être cherchés sur un échiquier 8x8. Par exemple des tours où les bonds 1 à 32 et 33 à 64 sont des bonds de cavalier alors que l'unique bond de 32 à 33 est quelconque (en respectant cependant un changement de couleur entre case 32 et 33). Ce sont des tours spéciaux appelés 2-kt magic tours. Comme on peut s'en douter, il y a beaucoup plus de tours de ce type que les 140 tours magiques.
Avec la même idée, on peut s'intéresser à des bonds spéciaux entre les bonds 16 et 17, 32 et 33 et 48 49. Un 4-kt tour est un tour de ce type. Le temps de calcul pour les trouver tous est très important. Une estimation est en cours ...
TANGRAM
Le même algorithm a été utilisé pour compter le nombre de placement des 11 pièces d'un TANGRAM hexagonal. Plusieurs adaptations ont du être faites car dans ce contexte, la position sur le tangram des pièces pouvant être posées dépend de la pose des pièces précédentes ce qui n'est pas le cas pour les déplacements de cavalier, les cases a atteindre étant connues à l'avance. Seul le critère libre ou occupé de la case doit être pris en compte.
Auteur : Yann DENEF mailto:ydenef@orange.fr