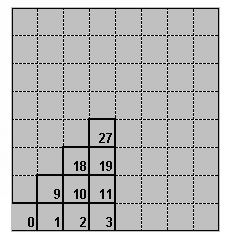
This page presents all the 280 Euler's magic squares . The solutions are obtained from 10 origins on the chess-board which allow by rotation and symmetry to obtain all the possibilities. These 10 boxes are called "starting zone ".
The squares of the chess-board are numbered from 0 to 63, from left to right and upwards. The starting zone includes squares 0,1,2,3,9,10,11,18,19,27

By several rotations and/or symmetries, each found solution generates 7 other solutions.
Moreover, each solution S, obtained from a given start, has a dual solution , whose origin is the last square of S, and whose way is exactly the opposite way of S. By a series of rotations and/or symmetries, the last square of a solution can be placed in the starting zone. From this square, one can thus obtain a solution which was already found: each solution is thus found 2 times. (there is no self-dual solution). There are thus only 140 independent solutions.
Among the 280 solutions, 126 are made of closed loops. A closed loop is a path whose last square, containing index 64 is far of one knight step from the first square containing index 1. In a closed loop, one can thus shift each square, the first square of index 1 becoming 2, the 2 becoming 3� square 63 becoming 64 and 64 becoming the first square of index 1. It is possible to make this operation 63 times to obtain 63 other solutions. All these "new" solutions do no form magic squares systematically.
However, it is noted that for certain solutions and particular values of shift, one obtains new magic squares. If the algorithm is correct, each of these "new" magic squares should no be new but must be after geometrical transformation, an already found solution. A simple tool was developed to correlate the whole of the solutions of closed loops. It produced the following tables.
The first line (8,16,24,32,40,48,56) indicates the shift values of the closed loops. Only multiple of 8 provide other magic squares. The solutions are noted x_y with x is the first square (in the starting zone) and y the rank of the solution found by the algorithm, i.e. its order of discovery. Ranks of the various solutions are presented thereafter in the summary tables. The first column lists the solutions of closed loops. Each line indicates the other associated solutions, the column indicating the value of the shift. When a solution was already associated, it does no appear any more in the first column. One obtains thus by line, families of solutions of closed loops. The results are presented in two tables: each line of the first table identifies the solutions (from one to five solutions), the dual solutions being indicated on the same line of the second table. Each table has 31 lines: there are only 31 distinct solutions among the 126 closed loop solutions.
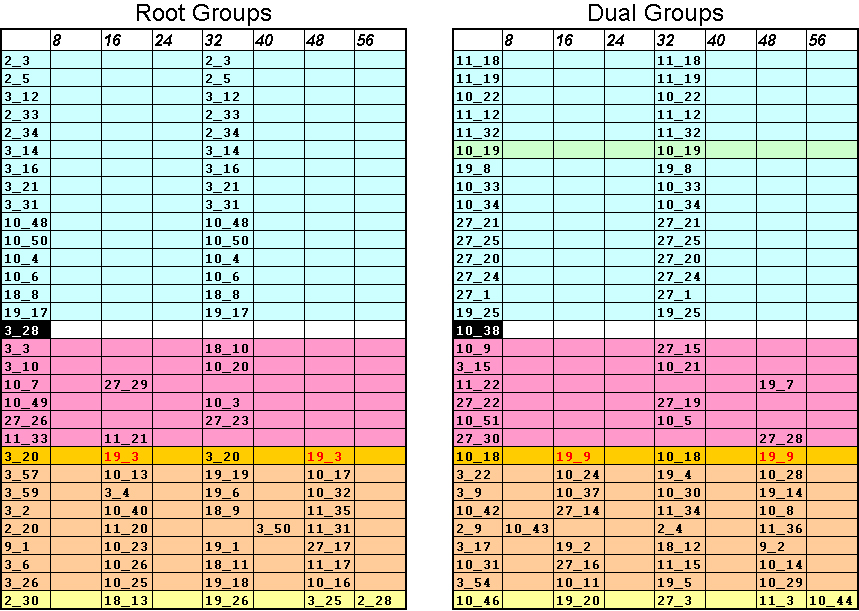
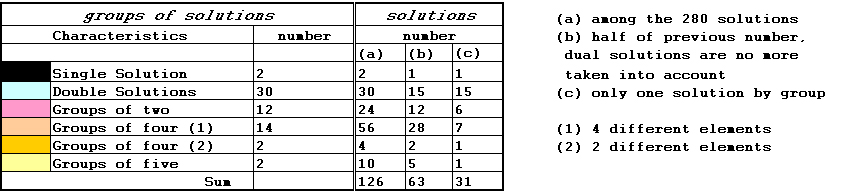
It is checked well that all the solutions obtained by shift had already been found directly. By taking account of these particular relations between closed loops, there are only 108 independent solutions, i.e. 108 solutions which do no have relations of symmetry or shift. These 108 solutions consist of 77 open solutions (the start square is no away from a jump to the last square) and of 31 closed solutions.
The following tables present all the magic solutions of Euler's Magic Kinght Tour. The research time for each solution is indicated in seconds. It's worth noting that there is no solution with unresolved dual associated, what tends to show that the algorithm traverses the totality of the tree of research (may be no bug). The algorithm is no very long but a bug is still possible.
The information contained in the tables of results is as follows:
Start : Start square
Sol. : Index of the solution
Time : Computing time to obtain the solution
DP Valeur of the principal diagonal A1-H8 (there is no magic square with magic diagonals)
DS : Value of the secondary diagonal H1-A8
SM : Semi Magic square (each 1/4 of the square is magic). There are 4 of them.
CT : Close Tour. The last square is from one step to start square.
End : Last square of the way.
Dual : Start square of the Duale solution, i.e. last square of the way placed in the starting zone.
Sol. : Index of the solution on the basis of the dual's start square solution
Time : Computing time (starting from the dual solution)
The evolutions of the search times starting from the 10 possible start squares
are indicated in another page.
Solutions are grouped by starting square. The time of the complete course of the chess-board, for each starting square is indicated to the beginning of each table. The solutions are classified by order of discovery. Times are expressed in seconds.
After each table of results, two chess-boards are presented. The position of the start square is green. The position of the last squares of the way is yellow. Each number indicates the number of distinct solutions leading to this square. When the way is a closed loop (closed tower), the square is violet (given provided by Harold Cataquet [ cataquet@ntlworld.com ]). The second chess-board presents all the arrivals brought back in the starting zone. It is noted that it is possible to obtain ways whose square of arrival is with some rotations and symmetries, the same one as the starting box. When the departure is on the diagonal (start 0, 9, 18, 27), all the second boxes of the found ways are located in the low half of the chess-board, on the right of the principal diagonal (A1-H8). The symmetrical ways neither are sought, nor presented.
One can decrease the total search time for all the magic squares starting from the 10 start squares of the starting zone while avoiding again seeking ways providing a last square already taken as start square, in a preceding research. Thus, whenever all ways are found from a given start square, the tree of search for the other solutions (from other start squares) are smaller. The new times obtained by applying this rule are indicated in this new table.
All solutions starting from each departure are grouped on one page. The indexes of these solutions are different from the indexes in the table because the table was constructed in the early 2000s using a single-threaded program, while the page groups the solutions using a multi-threaded program developed a few years later. Of course, the solutions are identical, only the numbering is different.All Magic solutions from start 0
| start 0 - # Solutions 9 ==== 1 146 284 Sec. ==== | ||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 0 | 1 | 7 453 | 292 | 236 | no | no | 58 | 2 | 31 | 200 511 |
| 0 | 2 | 60 370 | 292 | 206 | yes | no | 58 | 2 | 7 | 132 561 |
| 0 | 3 | 60 853 | 292 | 236 | yes | no | 58 | 2 | 8 | 132 561 |
| 0 | 4 | 703 085 | 282 | 210 | yes | no | 58 | 2 | 6 | 132 561 |
| 0 | 5 | 706 269 | 264 | 228 | no | no | 58 | 2 | 10 | 137 354 |
| 0 | 6 | 706 792 | 280 | 212 | no | no | 58 | 2 | 11 | 138 011 |
| 0 | 7 | 709 898 | 264 | 228 | no | no | 58 | 2 | 14 | 145 995 |
| 0 | 8 | 716 845 | 338 | 154 | no | no | 58 | 2 | 17 | 166 195 |
| 0 | 9 | 719 798 | 266 | 226 | yes | no | 58 | 2 | 21 | 175 572 |

All Magic solutions from start 1
| start 1 - # Solutions 7 ==== 695 006 Sec. ==== | ||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 1 | 1 | 306 872 | 322 | 246 | no | no | 59 | 3 | 33 | 128 594 |
| 1 | 2 | 306 872 | 322 | 216 | no | no | 59 | 3 | 38 | 129 053 |
| 1 | 3 | 307 175 | 352 | 246 | no | no | 59 | 3 | 34 | 128 594 |
| 1 | 4 | 307 175 | 352 | 216 | no | no | 59 | 3 | 39 | 129 053 |
| 1 | 5 | 378 530 | 300 | 370 | no | no | 59 | 3 | 35 | 128 594 |
| 1 | 6 | 378 530 | 300 | 340 | no | no | 59 | 3 | 40 | 129 054 |
| 1 | 7 | 489 757 | 152 | 376 | no | no | 59 | 3 | 1 | 84 607 |

All Magic solutions from start 2
| start 2 - # Solutions 37 ==== 658 633 sec. ==== | ||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 2 | 1 | 131 958 | 374 | 224 | no | no | 60 | 3 | 36 | 128 597 |
| 2 | 2 | 131 958 | 344 | 224 | no | no | 60 | 3 | 41 | 129 059 |
| 2 | 3 | 132 536 | 252 | 248 | no | yes | 12 | 11 | 18 | 74 718 |
| 2 | 4 | 132 538 | 222 | 184 | no | yes | 12 | 11 | 20 | 77 004 |
| 2 | 5 | 132 538 | 252 | 232 | no | yes | 12 | 11 | 19 | 77 000 |
| 2 | 6 | 132 561 | 310 | 238 | yes | no | 56 | 0 | 4 | 703 085 |
| 2 | 7 | 132 561 | 314 | 228 | yes | no | 56 | 0 | 2 | 60 370 |
| 2 | 8 | 132 561 | 284 | 228 | yes | no | 56 | 0 | 3 | 60 853 |
| 2 | 9 | 132 684 | 286 | 312 | no | yes | 12 | 11 | 31 | 93 902 |
| 2 | 10 | 137 354 | 292 | 256 | no | no | 56 | 0 | 5 | 706 269 |
| 2 | 11 | 138 011 | 308 | 240 | no | no | 56 | 0 | 6 | 706 792 |
| 2 | 12 | 138 755 | 374 | 258 | no | no | 60 | 3 | 37 | 128 597 |
| 2 | 13 | 138 755 | 344 | 258 | no | no | 60 | 3 | 42 | 129 059 |
| 2 | 14 | 145 995 | 292 | 256 | no | no | 56 | 0 | 7 | 709 898 |
| 2 | 15 | 150 405 | 204 | 324 | no | no | 58 | 2 | 16 | 150 405 |
| 2 | 16 | 150 405 | 196 | 316 | no | no | 58 | 2 | 15 | 150 405 |
| 2 | 17 | 166 195 | 366 | 182 | no | no | 56 | 0 | 8 | 716 845 |
| 2 | 18 | 166 281 | 288 | 312 | no | no | 21 | 18 | 6 | 54 058 |
| 2 | 19 | 167 247 | 352 | 248 | no | no | 21 | 18 | 1 | 52 662 |
| 2 | 20 | 167 483 | 208 | 234 | no | yes | 12 | 11 | 36 | 105 566 |
| 2 | 21 | 175 572 | 294 | 254 | yes | no | 56 | 0 | 9 | 719 798 |
| 2 | 22 | 181 453 | 272 | 278 | no | no | 23 | 2 | 35 | 602 068 |
| 2 | 23 | 181 453 | 272 | 318 | no | no | 28 | 27 | 6 | 13 655 |
| 2 | 24 | 181 453 | 258 | 318 | no | no | 28 | 27 | 11 | 20 511 |
| 2 | 25 | 181 574 | 272 | 328 | no | no | 21 | 18 | 2 | 52 667 |
| 2 | 26 | 181 575 | 272 | 328 | no | no | 28 | 27 | 7 | 13 655 |
| 2 | 27 | 181 575 | 258 | 328 | no | no | 28 | 27 | 12 | 20 511 |
| 2 | 28 | 196 639 | 320 | 200 | no | yes | 17 | 10 | 44 | 188 149 |
| 2 | 29 | 196 646 | 306 | 208 | no | no | 3 | 3 | 53 | 273 280 |
| 2 | 30 | 197 907 | 256 | 264 | no | yes | 12 | 11 | 3 | 68 137 |
| 2 | 31 | 200 511 | 284 | 228 | no | no | 56 | 0 | 1 | 7 453 |
| 2 | 32 | 203 761 | 276 | 258 | no | no | 35 | 27 | 27 | 138 295 |
| 2 | 33 | 203 829 | 264 | 248 | no | yes | 12 | 11 | 12 | 68 750 |
| 2 | 34 | 203 840 | 264 | 256 | no | yes | 12 | 11 | 32 | 101 843 |
| 2 | 35 | 602 068 | 242 | 248 | no | no | 40 | 2 | 22 | 181 453 |
| 2 | 36 | 605 912 | 228 | 344 | no | no | 35 | 27 | 18 | 39 993 |
| 2 | 37 | 624 529 | 184 | 336 | no | no | 49 | 9 | 6 | 64 182 |

All Magic solutions from start 3
|
start 3 - # Solutions 61 ==== 682 646 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 3 | 1 | 84 607 | 144 | 368 | no | no | 57 | 1 | 7 | 489 757 |
| 3 | 2 | 108 007 | 192 | 328 | no | yes | 13 | 10 | 8 | 155 864 |
| 3 | 3 | 108 076 | 202 | 318 | no | yes | 13 | 10 | 9 | 155 938 |
| 3 | 4 | 108 393 | 158 | 338 | no | yes | 13 | 10 | 37 | 167 243 |
| 3 | 5 | 108 393 | 158 | 338 | no | no | 4 | 3 | 27 | 119 708 |
| 3 | 6 | 108 394 | 202 | 318 | no | yes | 13 | 10 | 14 | 156 272 |
| 3 | 7 | 108 394 | 210 | 296 | no | no | 25 | 11 | 27 | 82 890 |
| 3 | 8 | 108 394 | 258 | 296 | no | no | 27 | 27 | 9 | 13 761 |
| 3 | 9 | 108 395 | 246 | 234 | no | yes | 20 | 19 | 6 | 14 540 |
| 3 | 10 | 108 845 | 216 | 304 | no | yes | 13 | 10 | 21 | 157 324 |
| 3 | 11 | 108 845 | 272 | 296 | no | no | 27 | 27 | 4 | 13 338 |
| 3 | 12 | 108 852 | 216 | 304 | no | yes | 13 | 10 | 22 | 157 324 |
| 3 | 13 | 109 043 | 224 | 296 | no | no | 25 | 11 | 10 | 68 666 |
| 3 | 14 | 109 486 | 216 | 304 | no | yes | 13 | 10 | 19 | 156 731 |
| 3 | 15 | 109 486 | 216 | 304 | no | yes | 13 | 10 | 20 | 156 736 |
| 3 | 16 | 109 486 | 216 | 288 | no | yes | 20 | 19 | 8 | 18 402 |
| 3 | 17 | 109 554 | 208 | 312 | no | yes | 13 | 10 | 23 | 157 406 |
| 3 | 18 | 110 621 | 168 | 284 | no | no | 4 | 3 | 58 | 278 855 |
| 3 | 19 | 110 621 | 272 | 246 | no | no | 27 | 27 | 13 | 20 605 |
| 3 | 20 | 110 622 | 248 | 244 | no | yes | 20 | 19 | 9 | 21 290 |
| 3 | 21 | 117 711 | 200 | 320 | no | yes | 13 | 10 | 33 | 165 465 |
| 3 | 22 | 119 598 | 168 | 348 | no | yes | 13 | 10 | 13 | 156 271 |
| 3 | 23 | 119 600 | 200 | 320 | no | no | 38 | 11 | 1 | 68 137 |
| 3 | 24 | 119 600 | 200 | 306 | no | no | 38 | 11 | 13 | 72 510 |
| 3 | 25 | 119 601 | 136 | 384 | no | yes | 13 | 10 | 46 | 188 941 |
| 3 | 26 | 119 708 | 182 | 362 | no | yes | 13 | 10 | 11 | 156 271 |
| 3 | 27 | 119 708 | 182 | 362 | no | no | 4 | 3 | 5 | 108 393 |
| 3 | 28 | 120 037 | 144 | 384 | no | yes | 13 | 10 | 38 | 167 589 |
| 3 | 29 | 120 037 | 144 | 384 | no | no | 4 | 3 | 30 | 120 037 |
| 3 | 30 | 120 037 | 136 | 376 | no | no | 4 | 3 | 29 | 120 037 |
| 3 | 31 | 121 214 | 208 | 320 | no | yes | 13 | 10 | 34 | 165 560 |
| 3 | 32 | 121 226 | 232 | 288 | no | no | 38 | 11 | 11 | 68 691 |
| 3 | 33 | 128 594 | 274 | 198 | no | no | 57 | 1 | 1 | 306 872 |
| 3 | 34 | 128 594 | 274 | 168 | no | no | 57 | 1 | 3 | 307 175 |
| 3 | 35 | 128 594 | 150 | 220 | no | no | 57 | 1 | 5 | 378 530 |
| 3 | 36 | 128 597 | 146 | 296 | no | no | 61 | 2 | 1 | 131 958 |
| 3 | 37 | 128 597 | 146 | 262 | no | no | 61 | 2 | 12 | 138 755 |
| 3 | 38 | 129 053 | 304 | 198 | no | no | 57 | 1 | 2 | 306 872 |
| 3 | 39 | 129 053 | 304 | 168 | no | no | 57 | 1 | 4 | 307 175 |
| 3 | 40 | 129 054 | 180 | 220 | no | no | 57 | 1 | 6 | 378 530 |
| 3 | 41 | 129 059 | 176 | 296 | no | no | 61 | 2 | 2 | 131 958 |
| 3 | 42 | 129 059 | 176 | 262 | no | no | 61 | 2 | 13 | 138 755 |
| 3 | 43 | 136 421 | 216 | 234 | no | no | 29 | 19 | 10 | 21 563 |
| 3 | 44 | 136 421 | 216 | 224 | no | no | 29 | 19 | 12 | 21 992 |
| 3 | 45 | 136 423 | 248 | 288 | no | no | 36 | 27 | 5 | 13 655 |
| 3 | 46 | 136 423 | 248 | 274 | no | no | 36 | 27 | 10 | 20 511 |
| 3 | 47 | 136 472 | 236 | 268 | no | no | 36 | 27 | 8 | 13 655 |
| 3 | 48 | 136 546 | 230 | 234 | no | no | 29 | 19 | 11 | 21 563 |
| 3 | 49 | 136 546 | 230 | 224 | no | no | 29 | 19 | 13 | 21 992 |
| 3 | 50 | 136 567 | 170 | 272 | no | yes | 13 | 10 | 43 | 182 823 |
| 3 | 51 | 137 207 | 216 | 274 | no | no | 32 | 3 | 61 | 503 264 |
| 3 | 52 | 137 207 | 216 | 264 | no | no | 34 | 19 | 15 | 22 236 |
| 3 | 53 | 273 280 | 214 | 312 | no | no | 2 | 2 | 29 | 196 646 |
| 3 | 54 | 278 744 | 222 | 338 | no | yes | 13 | 10 | 25 | 158 343 |
| 3 | 55 | 278 746 | 222 | 320 | no | no | 38 | 11 | 2 | 68 137 |
| 3 | 56 | 278 746 | 222 | 306 | no | no | 38 | 11 | 14 | 72 510 |
| 3 | 57 | 278 855 | 236 | 352 | no | yes | 13 | 10 | 24 | 158 343 |
| 3 | 58 | 278 855 | 236 | 352 | no | no | 4 | 3 | 18 | 110 621 |
| 3 | 59 | 279 481 | 222 | 338 | no | yes | 13 | 10 | 30 | 158 356 |
| 3 | 60 | 279 777 | 330 | 264 | no | no | 45 | 18 | 4 | 53 153 |
| 3 | 61 | 503 264 | 246 | 304 | no | no | 31 | 3 | 51 | 137 207 |

All Magic solutions from start 9
|
start 9 - # Solutions 6 ==== 190 851 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 9 | 1 | 56 965 | 184 | 208 | no | yes | 19 | 19 | 2 | 5 448 |
| 9 | 2 | 57 015 | 184 | 208 | no | yes | 19 | 19 | 1 | 5 418 |
| 9 | 3 | 57 258 | 240 | 280 | no | no | 14 | 9 | 4 | 57 778 |
| 9 | 4 | 57 778 | 240 | 280 | no | no | 14 | 9 | 3 | 57 258 |
| 9 | 5 | 60 780 | 208 | 256 | no | no | 37 | 19 | 16 | 31 528 |
| 9 | 6 | 64 182 | 184 | 336 | no | no | 58 | 2 | 37 | 624 529 |

All Magic solutions from start 10
|
start 10 - # Solutions 51 ==== 324 546 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 10 | 1 | 56 410 | 208 | 216 | no | no | 29 | 19 | 23 | 201 583 |
| 10 | 2 | 68 924 | 256 | 264 | no | no | 11 | 11 | 37 | 164 766 |
| 10 | 3 | 87 458 | 264 | 256 | no | yes | 27 | 27 | 19 | 91 999 |
| 10 | 4 | 87 458 | 264 | 256 | no | yes | 27 | 27 | 20 | 91 999 |
| 10 | 5 | 87 533 | 228 | 292 | no | yes | 27 | 27 | 23 | 124 318 |
| 10 | 6 | 87 533 | 228 | 292 | no | yes | 27 | 27 | 24 | 124 318 |
| 10 | 7 | 120 327 | 248 | 256 | no | yes | 25 | 11 | 22 | 80 277 |
| 10 | 8 | 155 864 | 192 | 328 | no | yes | 4 | 3 | 2 | 108 007 |
| 10 | 9 | 155 938 | 202 | 318 | no | yes | 4 | 3 | 3 | 108 076 |
| 10 | 10 | 156 271 | 158 | 338 | no | no | 13 | 10 | 36 | 167 243 |
| 10 | 11 | 156 271 | 158 | 338 | no | yes | 4 | 3 | 26 | 119 708 |
| 10 | 12 | 156 271 | 172 | 352 | no | no | 13 | 10 | 35 | 167 127 |
| 10 | 13 | 156 271 | 172 | 352 | no | yes | 4 | 3 | 22 | 119 598 |
| 10 | 14 | 156 272 | 202 | 318 | no | yes | 4 | 3 | 6 | 108 394 |
| 10 | 15 | 156 272 | 258 | 296 | no | no | 18 | 18 | 3 | 52 744 |
| 10 | 16 | 156 272 | 246 | 234 | no | yes | 20 | 19 | 5 | 14 522 |
| 10 | 17 | 156 272 | 236 | 224 | no | yes | 20 | 19 | 4 | 14 484 |
| 10 | 18 | 156 283 | 212 | 272 | no | yes | 20 | 19 | 3 | 14 206 |
| 10 | 19 | 156 731 | 216 | 304 | no | yes | 4 | 3 | 14 | 109 486 |
| 10 | 20 | 156 736 | 216 | 304 | no | yes | 4 | 3 | 15 | 109 486 |
| 10 | 21 | 157 324 | 216 | 304 | no | yes | 4 | 3 | 10 | 108 845 |
| 10 | 22 | 157 324 | 216 | 304 | no | yes | 4 | 3 | 12 | 108 852 |
| 10 | 23 | 157 406 | 208 | 312 | no | yes | 4 | 3 | 17 | 109 554 |
| 10 | 24 | 158 343 | 168 | 284 | no | yes | 4 | 3 | 57 | 278 855 |
| 10 | 25 | 158 343 | 182 | 298 | no | yes | 4 | 3 | 54 | 278 744 |
| 10 | 26 | 158 343 | 202 | 254 | no | yes | 25 | 11 | 15 | 72 511 |
| 10 | 27 | 158 343 | 296 | 250 | no | no | 13 | 10 | 47 | 194 526 |
| 10 | 28 | 158 343 | 296 | 220 | no | yes | 20 | 19 | 19 | 31 767 |
| 10 | 29 | 158 343 | 286 | 210 | no | yes | 20 | 19 | 18 | 31 731 |
| 10 | 30 | 158 356 | 182 | 298 | no | yes | 4 | 3 | 59 | 279 481 |
| 10 | 31 | 158 356 | 202 | 254 | no | yes | 25 | 11 | 17 | 72 556 |
| 10 | 32 | 158 357 | 286 | 210 | no | yes | 20 | 19 | 14 | 22 007 |
| 10 | 33 | 165 465 | 200 | 320 | no | yes | 4 | 3 | 21 | 117 711 |
| 10 | 34 | 165 560 | 200 | 312 | no | yes | 4 | 3 | 31 | 121 214 |
| 10 | 35 | 167 127 | 168 | 348 | no | no | 13 | 10 | 12 | 156 271 |
| 10 | 36 | 167 243 | 182 | 362 | no | no | 13 | 10 | 10 | 156 271 |
| 10 | 37 | 167 243 | 182 | 362 | no | yes | 4 | 3 | 4 | 108 393 |
| 10 | 38 | 167 589 | 136 | 376 | no | yes | 4 | 3 | 28 | 120 037 |
| 10 | 39 | 177 351 | 200 | 240 | no | no | 29 | 19 | 21 | 199 522 |
| 10 | 40 | 177 351 | 192 | 200 | no | yes | 25 | 11 | 34 | 105 408 |
| 10 | 41 | 177 386 | 200 | 240 | no | no | 29 | 19 | 22 | 200 503 |
| 10 | 42 | 177 386 | 192 | 200 | no | yes | 25 | 11 | 35 | 105 488 |
| 10 | 43 | 182 823 | 248 | 350 | no | yes | 4 | 3 | 50 | 136 567 |
| 10 | 44 | 188 149 | 200 | 320 | no | yes | 16 | 2 | 28 | 196 639 |
| 10 | 45 | 188 291 | 262 | 306 | no | no | 11 | 11 | 9 | 68 648 |
| 10 | 46 | 188 941 | 136 | 384 | no | yes | 4 | 3 | 25 | 119 601 |
| 10 | 47 | 194 526 | 270 | 224 | no | no | 13 | 10 | 27 | 158 343 |
| 10 | 48 | 211 636 | 264 | 256 | no | yes | 27 | 27 | 21 | 92 030 |
| 10 | 49 | 211 636 | 264 | 256 | no | yes | 27 | 27 | 22 | 92 030 |
| 10 | 50 | 211 717 | 228 | 292 | no | yes | 27 | 27 | 25 | 124 338 |
| 10 | 51 | 211 717 | 228 | 292 | no | yes | 27 | 27 | 26 | 124 338 |

All Magic solutions from start 11
|
start 11 - # Solutions 37 ==== 290 238 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 11 | 1 | 68 137 | 320 | 200 | no | no | 39 | 3 | 23 | 119 600 |
| 11 | 2 | 68 137 | 298 | 200 | no | no | 39 | 3 | 55 | 278 746 |
| 11 | 3 | 68 137 | 256 | 264 | no | yes | 5 | 2 | 30 | 197 907 |
| 11 | 4 | 68 140 | 342 | 178 | no | no | 51 | 11 | 23 | 82 842 |
| 11 | 5 | 68 156 | 342 | 178 | no | no | 51 | 11 | 24 | 82 857 |
| 11 | 6 | 68 158 | 320 | 200 | no | no | 51 | 11 | 25 | 82 858 |
| 11 | 7 | 68 201 | 312 | 208 | no | no | 51 | 11 | 28 | 82 897 |
| 11 | 8 | 68 577 | 216 | 304 | no | no | 35 | 27 | 2 | 2 088 |
| 11 | 9 | 68 648 | 258 | 214 | no | no | 10 | 10 | 45 | 188 291 |
| 11 | 10 | 68 666 | 296 | 224 | no | no | 24 | 3 | 13 | 109 043 |
| 11 | 11 | 68 691 | 288 | 232 | no | no | 39 | 3 | 32 | 121 226 |
| 11 | 12 | 68 750 | 272 | 256 | no | yes | 5 | 2 | 33 | 203 829 |
| 11 | 13 | 72 510 | 320 | 214 | no | no | 39 | 3 | 24 | 119 600 |
| 11 | 14 | 72 510 | 298 | 214 | no | no | 39 | 3 | 56 | 278 746 |
| 11 | 15 | 72 511 | 318 | 266 | no | yes | 17 | 10 | 26 | 158 343 |
| 11 | 16 | 72 531 | 320 | 218 | no | no | 51 | 11 | 26 | 82 858 |
| 11 | 17 | 72 556 | 318 | 266 | no | yes | 17 | 10 | 31 | 158 356 |
| 11 | 18 | 74 718 | 272 | 268 | no | yes | 5 | 2 | 3 | 132 536 |
| 11 | 19 | 77 000 | 288 | 268 | no | yes | 5 | 2 | 5 | 132 538 |
| 11 | 20 | 77 004 | 336 | 298 | no | yes | 5 | 2 | 4 | 132 538 |
| 11 | 21 | 80 276 | 272 | 264 | no | yes | 28 | 27 | 28 | 164 417 |
| 11 | 22 | 80 277 | 272 | 264 | no | yes | 17 | 10 | 7 | 120 327 |
| 11 | 23 | 82 842 | 342 | 178 | no | no | 51 | 11 | 4 | 68 140 |
| 11 | 24 | 82 857 | 342 | 178 | no | no | 51 | 11 | 5 | 68 156 |
| 11 | 25 | 82 858 | 320 | 200 | no | no | 51 | 11 | 6 | 68 158 |
| 11 | 26 | 82 858 | 302 | 200 | no | no | 51 | 11 | 16 | 72 531 |
| 11 | 27 | 82 890 | 310 | 224 | no | no | 24 | 3 | 7 | 108 394 |
| 11 | 28 | 82 897 | 312 | 208 | no | no | 51 | 11 | 7 | 68 201 |
| 11 | 29 | 87 243 | 240 | 280 | no | no | 51 | 11 | 30 | 87 681 |
| 11 | 30 | 87 681 | 240 | 280 | no | no | 51 | 11 | 29 | 87 243 |
| 11 | 31 | 93 902 | 208 | 234 | no | yes | 5 | 2 | 9 | 132 684 |
| 11 | 32 | 101 843 | 264 | 256 | no | yes | 5 | 2 | 34 | 203 840 |
| 11 | 33 | 101 914 | 272 | 264 | no | yes | 28 | 27 | 30 | 164 437 |
| 11 | 34 | 105 408 | 328 | 320 | no | yes | 17 | 10 | 40 | 177 351 |
| 11 | 35 | 105 488 | 328 | 320 | no | yes | 17 | 10 | 42 | 177 386 |
| 11 | 36 | 105 566 | 286 | 312 | no | yes | 5 | 2 | 20 | 167 483 |
| 11 | 37 | 164 766 | 264 | 256 | no | no | 10 | 10 | 2 | 68 924 |

All Magic solutions from start 18
|
start 18 - # Solutions 14 ==== 128 139 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 18 | 1 | 52 662 | 272 | 168 | no | no | 5 | 2 | 19 | 167 247 |
| 18 | 2 | 52 667 | 192 | 248 | no | no | 40 | 2 | 25 | 181 574 |
| 18 | 3 | 52 744 | 262 | 224 | no | no | 17 | 10 | 15 | 156 272 |
| 18 | 4 | 53 153 | 190 | 256 | no | no | 39 | 3 | 60 | 279 777 |
| 18 | 5 | 53 375 | 296 | 168 | no | no | 19 | 19 | 24 | 211 340 |
| 18 | 6 | 54 058 | 208 | 232 | no | no | 5 | 2 | 18 | 166 281 |
| 18 | 7 | 54 080 | 176 | 248 | no | no | 37 | 19 | 27 | 239 076 |
| 18 | 8 | 57 385 | 192 | 328 | no | yes | 35 | 27 | 1 | 2 088 |
| 18 | 9 | 57 410 | 200 | 320 | no | yes | 35 | 27 | 14 | 38 834 |
| 18 | 10 | 57 509 | 190 | 330 | no | yes | 35 | 27 | 15 | 38 931 |
| 18 | 11 | 57 704 | 190 | 330 | no | yes | 35 | 27 | 16 | 39 117 |
| 18 | 12 | 58 199 | 184 | 336 | no | yes | 35 | 27 | 17 | 39 584 |
| 18 | 13 | 58 601 | 128 | 392 | no | yes | 35 | 27 | 3 | 2 351 |
| 18 | 14 | 114 610 | 176 | 232 | no | no | 26 | 19 | 28 | 239 077 |

All Magic solutions from start 19
|
start 19 - # Solutions 28 ==== 321 107 Sec. ==== |
||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 19 | 1 | 5 418 | 336 | 312 | no | yes | 9 | 9 | 2 | 57 015 |
| 19 | 2 | 5 448 | 336 | 312 | no | yes | 9 | 9 | 1 | 56 965 |
| 19 | 3 | 14 206 | 248 | 308 | no | yes | 13 | 10 | 18 | 156 283 |
| 19 | 4 | 14 484 | 296 | 284 | no | yes | 13 | 10 | 17 | 156 272 |
| 19 | 5 | 14 522 | 286 | 274 | no | yes | 13 | 10 | 16 | 156 272 |
| 19 | 6 | 14 540 | 286 | 274 | no | yes | 4 | 3 | 9 | 108 395 |
| 19 | 7 | 16 984 | 264 | 272 | no | yes | 36 | 27 | 29 | 164 435 |
| 19 | 8 | 18 402 | 232 | 304 | no | yes | 4 | 3 | 16 | 109 486 |
| 19 | 9 | 21 290 | 276 | 272 | no | yes | 4 | 3 | 20 | 110 622 |
| 19 | 10 | 21 563 | 286 | 304 | no | no | 32 | 3 | 43 | 136 421 |
| 19 | 11 | 21 563 | 286 | 290 | no | no | 32 | 3 | 48 | 136 546 |
| 19 | 12 | 21 992 | 296 | 304 | no | no | 32 | 3 | 44 | 136 421 |
| 19 | 13 | 21 992 | 296 | 290 | no | no | 32 | 3 | 49 | 136 546 |
| 19 | 14 | 22 007 | 310 | 234 | no | yes | 13 | 10 | 32 | 158 357 |
| 19 | 15 | 22 236 | 256 | 304 | no | no | 31 | 3 | 52 | 137 207 |
| 19 | 16 | 31 528 | 312 | 264 | no | no | 54 | 9 | 5 | 60 780 |
| 19 | 17 | 31 555 | 264 | 256 | no | yes | 34 | 19 | 25 | 211 544 |
| 19 | 18 | 31 731 | 310 | 234 | no | yes | 13 | 10 | 29 | 158 343 |
| 19 | 19 | 31 767 | 300 | 224 | no | yes | 13 | 10 | 28 | 158 343 |
| 19 | 20 | 31 767 | 264 | 256 | no | yes | 34 | 19 | 26 | 211 880 |
| 19 | 21 | 199 522 | 280 | 320 | no | no | 41 | 10 | 39 | 177 351 |
| 19 | 22 | 200 503 | 280 | 320 | no | no | 41 | 10 | 41 | 177 386 |
| 19 | 23 | 201 583 | 304 | 312 | no | no | 41 | 10 | 1 | 56 410 |
| 19 | 24 | 211 340 | 224 | 352 | no | no | 18 | 18 | 5 | 53 375 |
| 19 | 25 | 211 544 | 264 | 256 | no | yes | 29 | 19 | 17 | 31 555 |
| 19 | 26 | 211 880 | 264 | 256 | no | yes | 29 | 19 | 20 | 31 767 |
| 19 | 27 | 239 076 | 344 | 272 | no | no | 45 | 18 | 7 | 54 080 |
| 19 | 28 | 239 077 | 344 | 288 | no | no | 18 | 18 | 14 | 114 610 |

All Magic solutions from start 27
| start 27 - # Solutions 30 ==== 198 763 Sec. ==== | ||||||||||
| Start |
Sol.
|
Time |
DP
|
DS
|
SM | CT | End | Dual | Sol. | Time |
| 27 | 1 | 2 088 | 192 | 328 | no | yes | 42 | 18 | 8 | 57 385 |
| 27 | 2 | 2 088 | 216 | 304 | no | no | 30 | 11 | 8 | 68 577 |
| 27 | 3 | 2 351 | 128 | 392 | no | yes | 42 | 18 | 13 | 58 601 |
| 27 | 4 | 13 338 | 248 | 224 | no | no | 24 | 3 | 11 | 108 845 |
| 27 | 5 | 13 655 | 272 | 232 | no | no | 39 | 3 | 45 | 136 423 |
| 27 | 6 | 13 655 | 202 | 248 | no | no | 40 | 2 | 23 | 181 453 |
| 27 | 7 | 13 655 | 192 | 248 | no | no | 40 | 2 | 26 | 181 575 |
| 27 | 8 | 13 655 | 284 | 252 | no | no | 39 | 3 | 47 | 136 472 |
| 27 | 9 | 13 761 | 262 | 224 | no | no | 24 | 3 | 8 | 108 394 |
| 27 | 10 | 20 511 | 272 | 246 | no | no | 39 | 3 | 46 | 136 423 |
| 27 | 11 | 20 511 | 202 | 262 | no | no | 40 | 2 | 24 | 181 453 |
| 27 | 12 | 20 511 | 192 | 262 | no | no | 40 | 2 | 27 | 181 575 |
| 27 | 13 | 20 605 | 248 | 274 | no | no | 24 | 3 | 19 | 110 621 |
| 27 | 14 | 38 834 | 200 | 320 | no | yes | 42 | 18 | 9 | 57 410 |
| 27 | 15 | 38 931 | 190 | 330 | no | yes | 42 | 18 | 10 | 57 509 |
| 27 | 16 | 39 117 | 190 | 330 | no | yes | 42 | 18 | 11 | 57 704 |
| 27 | 17 | 39 584 | 184 | 336 | no | yes | 42 | 18 | 12 | 58 199 |
| 27 | 18 | 39 993 | 176 | 292 | no | no | 58 | 2 | 36 | 605 912 |
| 27 | 19 | 91 999 | 256 | 264 | no | yes | 10 | 10 | 3 | 87 458 |
| 27 | 20 | 91 999 | 256 | 264 | no | yes | 10 | 10 | 4 | 87 458 |
| 27 | 21 | 92 030 | 256 | 264 | no | yes | 10 | 10 | 48 | 211 636 |
| 27 | 22 | 92 030 | 256 | 264 | no | yes | 10 | 10 | 49 | 211 636 |
| 27 | 23 | 124 318 | 292 | 228 | no | yes | 10 | 10 | 5 | 87 533 |
| 27 | 24 | 124 318 | 292 | 228 | no | yes | 10 | 10 | 6 | 87 533 |
| 27 | 25 | 124 338 | 292 | 228 | no | yes | 10 | 10 | 50 | 211 717 |
| 27 | 26 | 124 338 | 292 | 228 | no | yes | 10 | 10 | 51 | 211 717 |
| 27 | 27 | 138 295 | 262 | 244 | no | no | 58 | 2 | 32 | 203 761 |
| 27 | 28 | 164 417 | 256 | 248 | no | yes | 33 | 11 | 21 | 80 276 |
| 27 | 29 | 164 435 | 256 | 248 | no | yes | 44 | 19 | 7 | 16 984 |
| 27 | 30 | 164 437 | 256 | 248 | no | yes | 33 | 11 | 33 | 101 914 |
