
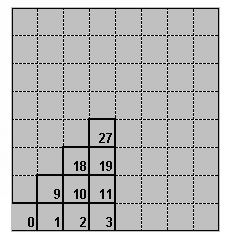
Cette page présente les 280 carrés magiques d'Euler. Les solutions sont recherchées à partir de 10 origines sur l'échiquier qui permettent par rotation et par symétrie d'obtenir toutes les possibilités. Ces 10 cases sont appelées "zone de départ". Les cases de l'échiquier sont numérotées de 0 à 63, de gauche vers la droite et ligne par ligne. La zone de départ comprend les cases 0,1,2,3,9,10,11,18,19,27
Ces 280 solutions ne sont pas indépendantes.
Par une série de rotations et de symétries axiales, chaque
solution trouvée génère 7 autres solutions.
De plus, chaque solution S, obtenue a partir d'une origine donnée, possède une solution duale S', dont l'origine est la case d'arrivée de S, et dont le chemin est exactement le chemin inverse de S. Par une série de rotations et de symétries, la case d'arrivée d'une solution peut être placée dans la zone de départ. En partant de cette case, on peut donc obtenir une solution qui a déjà été trouvée : chaque solution est donc trouvée 2 fois. (il n'y a pas de solution auto-duale)
Parmi les 280 solutions trouvées, 126 sont formées de chemins fermés. Un chemin fermé est un chemin dont la dernière case, contenant l'index 64 est à un saut de cavalier de la case de départ contenant l'index 1. Dans un chemin fermé, on peut ainsi décaler chacune des cases, la case de départ d'index 1 devenant 2, la 2 devenant 3 ... la case 63 devenant 64 et la case 64 devenant la case de départ d'index 1. Il est possible de faire cette opération 63 fois pour obtenir 63 autres solutions. Toutes ces "nouvelles" solutions ne forment pas systématiquement de carrés magiques.
Cependant, on constate que pour certaines solutions et pour des valeurs particulières de décalage, on obtient de nouveaux carrés magiques. Si l'algorithme est correct, tous ces "nouveaux" carrés magiques ne doivent pas être nouveaux mais doivent correspondre, après symétrie et rotation, à des solutions déjà trouvées. Un outil simple a été développé pour corréler l'ensemble des solutions de chemins fermés. Il a produit les tableaux suivants.
La première ligne (8,16,24,32,40,48,56) indique les valeurs de décalage sur les chemins fermés. Seuls, des décalages multiples de 8 fournissent d'autres carrés magiques. Les solutions sont notées x_y ou x est la case de départ (dans la zone de départ) et y le rang de la solution trouvée par l'algorithme, c'est à dire son ordre de découverte. Les rangs des différentes solutions sont présentés par la suite dans les tableaux récapitulatifs. La première colonne liste les solutions de chemins fermés. Chaque ligne indique les autres solutions associées, la colonne indiquant la valeur du décalage. Lorsqu'une solution a été associée, elle ne figure plus dans la première colonne. On obtient ainsi par ligne, des familles de solutions de chemins fermés. Les résultats sont présentés dans deux tableaux : chaque ligne du premier tableau identifie des solutions (de une à cinq solutions), les solutions duales étant indiquées sur la même ligne du second tableau. Chacun des tableaux a 31 lignes : il n'y a que 31 solutions distinctes parmi les 126 solutions de chemin fermé.
On vérifie bien que toutes les solutions obtenues par décalage avaient déjà été trouvées directement.


En tenant compte de ces relations particulières entre chemins fermés, il n'y a que 108 solutions indépendantes, c'est à dire 108 solutions qui n'ont pas de relations de symétrie ou de décalage. Ces 108 solutions sont constituées de 77 solutions ouvertes (l'arrivée n'est pas à un bon de cavalier du départ) et de 31 solutions fermées (l'arrivée est à un bond de cavalier du départ)
Les tableaux suivants présentent toutes les solutions de carrés magiques d'Euler. Le temps mis par l'algorithme de recherche pour obtenir la solution est indiqué en secondes. chaque solution est associée à sa solution duale. On constate qu'il n'y a pas de solution sans solution duale associé ce qui tend à montrer que l'algorithme parcourt la totalité de l'arbre de recherche. Les informations contenues dans les tableaux de résultats sont les suivantes :
Start : case de départ
Sol. : Index de la solution
Time : Temps de calcul pour obtenir la solution
DP Valeur de la diagonale principale (il n'y a pas de carré magique avec des diagonales magiques)
DS : Valeur de la diagonale secondaire
SM : Carré Semi magique (chaque 1/4 du carré est magique). Il y en a 4.
CT : Close Tour. L'arrivée est à un saut de cavalier du départ.
End : Case d'arrivée.
Dual : Case de départ de la solution Duale, c'est à dire case d'arrivée placée dans la zone de départ.
Sol. : Index de la solution en partant du départ de la solution duale
Time : Temps de calcul (à partir du départ de la solution duale)
Les évolutions des temps de recherche à partir des 10 départs
possibles sont indiquées dans une autre
page.
Cette page présente les solutions trouvées. Elles sont groupées par case de départ. Le temps du parcours complet de l'échiquier, pour chacune des cases de départ est indiqué au début de chaque tableau. Les solutions sont classées par ordre de découverte. Les temps sont exprimés en secondes.
Après chaque tableau de résultats, deux échiquiers sont présentés. Le premier présente en vert la position de la case de départ et en jaune la position des cases d'arrivée. Chaque nombre indique le nombre de solutions distinctes aboutissant à cette case. Lorsque le chemin est un chemin fermé (close tour), la case est violette (données fournies par Harold Cataquet [cataquet@ntlworld.com]). Le second échiquier présente toutes les arrivées ramenées dans la zone de départ. On constate qu'il est possible d'obtenir des chemins dont la case d'arrivée est à quelques rotations et symétries prés, la même que la case de départ. Lorsque le départ est sur la diagonale (start 0, 9, 18, 27), toutes les secondes cases des chemins trouvés se situent dans la moitié basse de l'échiquier, à droite de la diagonale principale (A1-H8). Les chemins symétriques ne sont ni recherchés, ni présentés.
On peut diminuer le temps de recherche global pour tous les carrés magiques à partir des 10 départs de la zone de départ en évitant de rechercher à nouveau des chemins dont la case d'arrivée à déjà été prise, lors d'une recherche précédente comme case de départ. Ainsi, au fur et à mesures que les chemins sont trouvés, l'arbre de recherche des solutions est de plus en plus petit. Les nouveaux temps obtenus en appliquant ce principe sont indiqués dans ce nouveau tableau.
Toutes les solutions à partir de chaque départ sont regroupées sur une page. Les index de ces solutions sont différents des index du tableau car le tableau a été construit au début des années 2000 à partir d'un programme mono-thread alors que la page regroupe les solutions à partir d'un autre programme multi-thread développé quelques années plus tard. Les solutions sont bien sûr identiques, seule la numérotation est différente.Toutes les solutions à partir du départ 0
| start 0 - # Solutions 9 ==== 1 146 284 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 0 | 7 453 | 292 | 236 | non | non | 58 | 2 | 31 | 200 511 | |
| 0 | 60 370 | 292 | 206 | oui | non | 58 | 2 | 7 | 132 561 | |
| 0 | 60 853 | 292 | 236 | oui | non | 58 | 2 | 8 | 132 561 | |
| 0 | 703 085 | 282 | 210 | oui | non | 58 | 2 | 6 | 132 561 | |
| 0 | 706 269 | 264 | 228 | non | non | 58 | 2 | 10 | 137 354 | |
| 0 | 706 792 | 280 | 212 | non | non | 58 | 2 | 11 | 138 011 | |
| 0 | 709 898 | 264 | 228 | non | non | 58 | 2 | 14 | 145 995 | |
| 0 | 716 845 | 338 | 154 | non | non | 58 | 2 | 17 | 166 195 | |
| 0 | 719 798 | 266 | 226 | oui | non | 58 | 2 | 21 | 175 572 | |

Toutes les solutions à partir du départ 1
| start 1 - # Solutions 7 ==== 695 006 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 1 | 1 | 306 872 | 322 | 246 | non | non | 59 | 3 | 33 | 128 594 |
| 1 | 2 | 306 872 | 322 | 216 | non | non | 59 | 3 | 38 | 129 053 |
| 1 | 3 | 307 175 | 352 | 246 | non | non | 59 | 3 | 34 | 128 594 |
| 1 | 4 | 307 175 | 352 | 216 | non | non | 59 | 3 | 39 | 129 053 |
| 1 | 5 | 378 530 | 300 | 370 | non | non | 59 | 3 | 35 | 128 594 |
| 1 | 6 | 378 530 | 300 | 340 | non | non | 59 | 3 | 40 | 129 054 |
| 1 | 7 | 489 757 | 152 | 376 | non | non | 59 | 3 | 1 | 84 607 |

Toutes les solutions à partir du départ 2
| start 2 - # Solutions 37 ==== 658 633 sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 2 | 1 | 131 958 | 374 | 224 | non | non | 60 | 3 | 36 | 128 597 |
| 2 | 2 | 131 958 | 344 | 224 | non | non | 60 | 3 | 41 | 129 059 |
| 2 | 3 | 132 536 | 252 | 248 | non | oui | 12 | 11 | 18 | 74 718 |
| 2 | 4 | 132 538 | 222 | 184 | non | oui | 12 | 11 | 20 | 77 004 |
| 2 | 5 | 132 538 | 252 | 232 | non | oui | 12 | 11 | 19 | 77 000 |
| 2 | 6 | 132 561 | 310 | 238 | oui | non | 56 | 0 | 4 | 703 085 |
| 2 | 7 | 132 561 | 314 | 228 | oui | non | 56 | 0 | 2 | 60 370 |
| 2 | 8 | 132 561 | 284 | 228 | oui | non | 56 | 0 | 3 | 60 853 |
| 2 | 9 | 132 684 | 286 | 312 | non | oui | 12 | 11 | 31 | 93 902 |
| 2 | 10 | 137 354 | 292 | 256 | non | non | 56 | 0 | 5 | 706 269 |
| 2 | 11 | 138 011 | 308 | 240 | non | non | 56 | 0 | 6 | 706 792 |
| 2 | 12 | 138 755 | 374 | 258 | non | non | 60 | 3 | 37 | 128 597 |
| 2 | 13 | 138 755 | 344 | 258 | non | non | 60 | 3 | 42 | 129 059 |
| 2 | 14 | 145 995 | 292 | 256 | non | non | 56 | 0 | 7 | 709 898 |
| 2 | 15 | 150 405 | 204 | 324 | non | non | 58 | 2 | 16 | 150 405 |
| 2 | 16 | 150 405 | 196 | 316 | non | non | 58 | 2 | 15 | 150 405 |
| 2 | 17 | 166 195 | 366 | 182 | non | non | 56 | 0 | 8 | 716 845 |
| 2 | 18 | 166 281 | 288 | 312 | non | non | 21 | 18 | 6 | 54 058 |
| 2 | 19 | 167 247 | 352 | 248 | non | non | 21 | 18 | 1 | 52 662 |
| 2 | 20 | 167 483 | 208 | 234 | non | oui | 12 | 11 | 36 | 105 566 |
| 2 | 21 | 175 572 | 294 | 254 | oui | non | 56 | 0 | 9 | 719 798 |
| 2 | 22 | 181 453 | 272 | 278 | non | non | 23 | 2 | 35 | 602 068 |
| 2 | 23 | 181 453 | 272 | 318 | non | non | 28 | 27 | 6 | 13 655 |
| 2 | 24 | 181 453 | 258 | 318 | non | non | 28 | 27 | 11 | 20 511 |
| 2 | 25 | 181 574 | 272 | 328 | non | non | 21 | 18 | 2 | 52 667 |
| 2 | 26 | 181 575 | 272 | 328 | non | non | 28 | 27 | 7 | 13 655 |
| 2 | 27 | 181 575 | 258 | 328 | non | non | 28 | 27 | 12 | 20 511 |
| 2 | 28 | 196 639 | 320 | 200 | non | oui | 17 | 10 | 44 | 188 149 |
| 2 | 29 | 196 646 | 306 | 208 | non | non | 3 | 3 | 53 | 273 280 |
| 2 | 30 | 197 907 | 256 | 264 | non | oui | 12 | 11 | 3 | 68 137 |
| 2 | 31 | 200 511 | 284 | 228 | non | non | 56 | 0 | 1 | 7 453 |
| 2 | 32 | 203 761 | 276 | 258 | non | non | 35 | 27 | 27 | 138 295 |
| 2 | 33 | 203 829 | 264 | 248 | non | oui | 12 | 11 | 12 | 68 750 |
| 2 | 34 | 203 840 | 264 | 256 | non | oui | 12 | 11 | 32 | 101 843 |
| 2 | 35 | 602 068 | 242 | 248 | non | non | 40 | 2 | 22 | 181 453 |
| 2 | 36 | 605 912 | 228 | 344 | non | non | 35 | 27 | 18 | 39 993 |
| 2 | 37 | 624 529 | 184 | 336 | non | non | 49 | 9 | 6 | 64 182 |

Toutes les solutions à partir du départ 3
| start 3 - # Solutions 61 ==== 682 646 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 3 | 1 | 84 607 | 144 | 368 | non | non | 57 | 1 | 7 | 489 757 |
| 3 | 2 | 108 007 | 192 | 328 | non | oui | 13 | 10 | 8 | 155 864 |
| 3 | 3 | 108 076 | 202 | 318 | non | oui | 13 | 10 | 9 | 155 938 |
| 3 | 4 | 108 393 | 158 | 338 | non | oui | 13 | 10 | 37 | 167 243 |
| 3 | 5 | 108 393 | 158 | 338 | non | non | 4 | 3 | 27 | 119 708 |
| 3 | 6 | 108 394 | 202 | 318 | non | oui | 13 | 10 | 14 | 156 272 |
| 3 | 7 | 108 394 | 210 | 296 | non | non | 25 | 11 | 27 | 82 890 |
| 3 | 8 | 108 394 | 258 | 296 | non | non | 27 | 27 | 9 | 13 761 |
| 3 | 9 | 108 395 | 246 | 234 | non | oui | 20 | 19 | 6 | 14 540 |
| 3 | 10 | 108 845 | 216 | 304 | non | oui | 13 | 10 | 21 | 157 324 |
| 3 | 11 | 108 845 | 272 | 296 | non | non | 27 | 27 | 4 | 13 338 |
| 3 | 12 | 108 852 | 216 | 304 | non | oui | 13 | 10 | 22 | 157 324 |
| 3 | 13 | 109 043 | 224 | 296 | non | non | 25 | 11 | 10 | 68 666 |
| 3 | 14 | 109 486 | 216 | 304 | non | oui | 13 | 10 | 19 | 156 731 |
| 3 | 15 | 109 486 | 216 | 304 | non | oui | 13 | 10 | 20 | 156 736 |
| 3 | 16 | 109 486 | 216 | 288 | non | oui | 20 | 19 | 8 | 18 402 |
| 3 | 17 | 109 554 | 208 | 312 | non | oui | 13 | 10 | 23 | 157 406 |
| 3 | 18 | 110 621 | 168 | 284 | non | non | 4 | 3 | 58 | 278 855 |
| 3 | 19 | 110 621 | 272 | 246 | non | non | 27 | 27 | 13 | 20 605 |
| 3 | 20 | 110 622 | 248 | 244 | non | oui | 20 | 19 | 9 | 21 290 |
| 3 | 21 | 117 711 | 200 | 320 | non | oui | 13 | 10 | 33 | 165 465 |
| 3 | 22 | 119 598 | 168 | 348 | non | oui | 13 | 10 | 13 | 156 271 |
| 3 | 23 | 119 600 | 200 | 320 | non | non | 38 | 11 | 1 | 68 137 |
| 3 | 24 | 119 600 | 200 | 306 | non | non | 38 | 11 | 13 | 72 510 |
| 3 | 25 | 119 601 | 136 | 384 | non | oui | 13 | 10 | 46 | 188 941 |
| 3 | 26 | 119 708 | 182 | 362 | non | oui | 13 | 10 | 11 | 156 271 |
| 3 | 27 | 119 708 | 182 | 362 | non | non | 4 | 3 | 5 | 108 393 |
| 3 | 28 | 120 037 | 144 | 384 | non | oui | 13 | 10 | 38 | 167 589 |
| 3 | 29 | 120 037 | 144 | 384 | non | non | 4 | 3 | 30 | 120 037 |
| 3 | 30 | 120 037 | 136 | 376 | non | non | 4 | 3 | 29 | 120 037 |
| 3 | 31 | 121 214 | 208 | 320 | non | oui | 13 | 10 | 34 | 165 560 |
| 3 | 32 | 121 226 | 232 | 288 | non | non | 38 | 11 | 11 | 68 691 |
| 3 | 33 | 128 594 | 274 | 198 | non | non | 57 | 1 | 1 | 306 872 |
| 3 | 34 | 128 594 | 274 | 168 | non | non | 57 | 1 | 3 | 307 175 |
| 3 | 35 | 128 594 | 150 | 220 | non | non | 57 | 1 | 5 | 378 530 |
| 3 | 36 | 128 597 | 146 | 296 | non | non | 61 | 2 | 1 | 131 958 |
| 3 | 37 | 128 597 | 146 | 262 | non | non | 61 | 2 | 12 | 138 755 |
| 3 | 38 | 129 053 | 304 | 198 | non | non | 57 | 1 | 2 | 306 872 |
| 3 | 39 | 129 053 | 304 | 168 | non | non | 57 | 1 | 4 | 307 175 |
| 3 | 40 | 129 054 | 180 | 220 | non | non | 57 | 1 | 6 | 378 530 |
| 3 | 41 | 129 059 | 176 | 296 | non | non | 61 | 2 | 2 | 131 958 |
| 3 | 42 | 129 059 | 176 | 262 | non | non | 61 | 2 | 13 | 138 755 |
| 3 | 43 | 136 421 | 216 | 234 | non | non | 29 | 19 | 10 | 21 563 |
| 3 | 44 | 136 421 | 216 | 224 | non | non | 29 | 19 | 12 | 21 992 |
| 3 | 45 | 136 423 | 248 | 288 | non | non | 36 | 27 | 5 | 13 655 |
| 3 | 46 | 136 423 | 248 | 274 | non | non | 36 | 27 | 10 | 20 511 |
| 3 | 47 | 136 472 | 236 | 268 | non | non | 36 | 27 | 8 | 13 655 |
| 3 | 48 | 136 546 | 230 | 234 | non | non | 29 | 19 | 11 | 21 563 |
| 3 | 49 | 136 546 | 230 | 224 | non | non | 29 | 19 | 13 | 21 992 |
| 3 | 50 | 136 567 | 170 | 272 | non | oui | 13 | 10 | 43 | 182 823 |
| 3 | 51 | 137 207 | 216 | 274 | non | non | 32 | 3 | 61 | 503 264 |
| 3 | 52 | 137 207 | 216 | 264 | non | non | 34 | 19 | 15 | 22 236 |
| 3 | 53 | 273 280 | 214 | 312 | non | non | 2 | 2 | 29 | 196 646 |
| 3 | 54 | 278 744 | 222 | 338 | non | oui | 13 | 10 | 25 | 158 343 |
| 3 | 55 | 278 746 | 222 | 320 | non | non | 38 | 11 | 2 | 68 137 |
| 3 | 56 | 278 746 | 222 | 306 | non | non | 38 | 11 | 14 | 72 510 |
| 3 | 57 | 278 855 | 236 | 352 | non | oui | 13 | 10 | 24 | 158 343 |
| 3 | 58 | 278 855 | 236 | 352 | non | non | 4 | 3 | 18 | 110 621 |
| 3 | 59 | 279 481 | 222 | 338 | non | oui | 13 | 10 | 30 | 158 356 |
| 3 | 60 | 279 777 | 330 | 264 | non | non | 45 | 18 | 4 | 53 153 |
| 3 | 61 | 503 264 | 246 | 304 | non | non | 31 | 3 | 51 | 137 207 |

Toutes les solutions à partir du départ 9
| start 9 - # Solutions 6 ==== 190 851 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 9 | 1 | 56 965 | 184 | 208 | non | oui | 19 | 19 | 2 | 5 448 |
| 9 | 2 | 57 015 | 184 | 208 | non | oui | 19 | 19 | 1 | 5 418 |
| 9 | 3 | 57 258 | 240 | 280 | non | non | 14 | 9 | 4 | 57 778 |
| 9 | 4 | 57 778 | 240 | 280 | non | non | 14 | 9 | 3 | 57 258 |
| 9 | 5 | 60 780 | 208 | 256 | non | non | 37 | 19 | 16 | 31 528 |
| 9 | 6 | 64 182 | 184 | 336 | non | non | 58 | 2 | 37 | 624 529 |

Toutes les solutions à partir du départ 10
| start 10 - # Solutions 51 ==== 324 546 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 10 | 1 | 56 410 | 208 | 216 | non | non | 29 | 19 | 23 | 201 583 |
| 10 | 2 | 68 924 | 256 | 264 | non | non | 11 | 11 | 37 | 164 766 |
| 10 | 3 | 87 458 | 264 | 256 | non | oui | 27 | 27 | 19 | 91 999 |
| 10 | 4 | 87 458 | 264 | 256 | non | oui | 27 | 27 | 20 | 91 999 |
| 10 | 5 | 87 533 | 228 | 292 | non | oui | 27 | 27 | 23 | 124 318 |
| 10 | 6 | 87 533 | 228 | 292 | non | oui | 27 | 27 | 24 | 124 318 |
| 10 | 7 | 120 327 | 248 | 256 | non | oui | 25 | 11 | 22 | 80 277 |
| 10 | 8 | 155 864 | 192 | 328 | non | oui | 4 | 3 | 2 | 108 007 |
| 10 | 9 | 155 938 | 202 | 318 | non | oui | 4 | 3 | 3 | 108 076 |
| 10 | 10 | 156 271 | 158 | 338 | non | non | 13 | 10 | 36 | 167 243 |
| 10 | 11 | 156 271 | 158 | 338 | non | oui | 4 | 3 | 26 | 119 708 |
| 10 | 12 | 156 271 | 172 | 352 | non | non | 13 | 10 | 35 | 167 127 |
| 10 | 13 | 156 271 | 172 | 352 | non | oui | 4 | 3 | 22 | 119 598 |
| 10 | 14 | 156 272 | 202 | 318 | non | oui | 4 | 3 | 6 | 108 394 |
| 10 | 15 | 156 272 | 258 | 296 | non | non | 18 | 18 | 3 | 52 744 |
| 10 | 16 | 156 272 | 246 | 234 | non | oui | 20 | 19 | 5 | 14 522 |
| 10 | 17 | 156 272 | 236 | 224 | non | oui | 20 | 19 | 4 | 14 484 |
| 10 | 18 | 156 283 | 212 | 272 | non | oui | 20 | 19 | 3 | 14 206 |
| 10 | 19 | 156 731 | 216 | 304 | non | oui | 4 | 3 | 14 | 109 486 |
| 10 | 20 | 156 736 | 216 | 304 | non | oui | 4 | 3 | 15 | 109 486 |
| 10 | 21 | 157 324 | 216 | 304 | non | oui | 4 | 3 | 10 | 108 845 |
| 10 | 22 | 157 324 | 216 | 304 | non | oui | 4 | 3 | 12 | 108 852 |
| 10 | 23 | 157 406 | 208 | 312 | non | oui | 4 | 3 | 17 | 109 554 |
| 10 | 24 | 158 343 | 168 | 284 | non | oui | 4 | 3 | 57 | 278 855 |
| 10 | 25 | 158 343 | 182 | 298 | non | oui | 4 | 3 | 54 | 278 744 |
| 10 | 26 | 158 343 | 202 | 254 | non | oui | 25 | 11 | 15 | 72 511 |
| 10 | 27 | 158 343 | 296 | 250 | non | non | 13 | 10 | 47 | 194 526 |
| 10 | 28 | 158 343 | 296 | 220 | non | oui | 20 | 19 | 19 | 31 767 |
| 10 | 29 | 158 343 | 286 | 210 | non | oui | 20 | 19 | 18 | 31 731 |
| 10 | 30 | 158 356 | 182 | 298 | non | oui | 4 | 3 | 59 | 279 481 |
| 10 | 31 | 158 356 | 202 | 254 | non | oui | 25 | 11 | 17 | 72 556 |
| 10 | 32 | 158 357 | 286 | 210 | non | oui | 20 | 19 | 14 | 22 007 |
| 10 | 33 | 165 465 | 200 | 320 | non | oui | 4 | 3 | 21 | 117 711 |
| 10 | 34 | 165 560 | 200 | 312 | non | oui | 4 | 3 | 31 | 121 214 |
| 10 | 35 | 167 127 | 168 | 348 | non | non | 13 | 10 | 12 | 156 271 |
| 10 | 36 | 167 243 | 182 | 362 | non | non | 13 | 10 | 10 | 156 271 |
| 10 | 37 | 167 243 | 182 | 362 | non | oui | 4 | 3 | 4 | 108 393 |
| 10 | 38 | 167 589 | 136 | 376 | non | oui | 4 | 3 | 28 | 120 037 |
| 10 | 39 | 177 351 | 200 | 240 | non | non | 29 | 19 | 21 | 199 522 |
| 10 | 40 | 177 351 | 192 | 200 | non | oui | 25 | 11 | 34 | 105 408 |
| 10 | 41 | 177 386 | 200 | 240 | non | non | 29 | 19 | 22 | 200 503 |
| 10 | 42 | 177 386 | 192 | 200 | non | oui | 25 | 11 | 35 | 105 488 |
| 10 | 43 | 182 823 | 248 | 350 | non | oui | 4 | 3 | 50 | 136 567 |
| 10 | 44 | 188 149 | 200 | 320 | non | oui | 16 | 2 | 28 | 196 639 |
| 10 | 45 | 188 291 | 262 | 306 | non | non | 11 | 11 | 9 | 68 648 |
| 10 | 46 | 188 941 | 136 | 384 | non | oui | 4 | 3 | 25 | 119 601 |
| 10 | 47 | 194 526 | 270 | 224 | non | non | 13 | 10 | 27 | 158 343 |
| 10 | 48 | 211 636 | 264 | 256 | non | oui | 27 | 27 | 21 | 92 030 |
| 10 | 49 | 211 636 | 264 | 256 | non | oui | 27 | 27 | 22 | 92 030 |
| 10 | 50 | 211 717 | 228 | 292 | non | oui | 27 | 27 | 25 | 124 338 |
| 10 | 51 | 211 717 | 228 | 292 | non | oui | 27 | 27 | 26 | 124 338 |

Toutes les solutions à partir du départ 11
| start 11 - # Solutions 37 ==== 290 238 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 11 | 1 | 68 137 | 320 | 200 | non | non | 39 | 3 | 23 | 119 600 |
| 11 | 2 | 68 137 | 298 | 200 | non | non | 39 | 3 | 55 | 278 746 |
| 11 | 3 | 68 137 | 256 | 264 | non | oui | 5 | 2 | 30 | 197 907 |
| 11 | 4 | 68 140 | 342 | 178 | non | non | 51 | 11 | 23 | 82 842 |
| 11 | 5 | 68 156 | 342 | 178 | non | non | 51 | 11 | 24 | 82 857 |
| 11 | 6 | 68 158 | 320 | 200 | non | non | 51 | 11 | 25 | 82 858 |
| 11 | 7 | 68 201 | 312 | 208 | non | non | 51 | 11 | 28 | 82 897 |
| 11 | 8 | 68 577 | 216 | 304 | non | non | 35 | 27 | 2 | 2 088 |
| 11 | 9 | 68 648 | 258 | 214 | non | non | 10 | 10 | 45 | 188 291 |
| 11 | 10 | 68 666 | 296 | 224 | non | non | 24 | 3 | 13 | 109 043 |
| 11 | 11 | 68 691 | 288 | 232 | non | non | 39 | 3 | 32 | 121 226 |
| 11 | 12 | 68 750 | 272 | 256 | non | oui | 5 | 2 | 33 | 203 829 |
| 11 | 13 | 72 510 | 320 | 214 | non | non | 39 | 3 | 24 | 119 600 |
| 11 | 14 | 72 510 | 298 | 214 | non | non | 39 | 3 | 56 | 278 746 |
| 11 | 15 | 72 511 | 318 | 266 | non | oui | 17 | 10 | 26 | 158 343 |
| 11 | 16 | 72 531 | 320 | 218 | non | non | 51 | 11 | 26 | 82 858 |
| 11 | 17 | 72 556 | 318 | 266 | non | oui | 17 | 10 | 31 | 158 356 |
| 11 | 18 | 74 718 | 272 | 268 | non | oui | 5 | 2 | 3 | 132 536 |
| 11 | 19 | 77 000 | 288 | 268 | non | oui | 5 | 2 | 5 | 132 538 |
| 11 | 20 | 77 004 | 336 | 298 | non | oui | 5 | 2 | 4 | 132 538 |
| 11 | 21 | 80 276 | 272 | 264 | non | oui | 28 | 27 | 28 | 164 417 |
| 11 | 22 | 80 277 | 272 | 264 | non | oui | 17 | 10 | 7 | 120 327 |
| 11 | 23 | 82 842 | 342 | 178 | non | non | 51 | 11 | 4 | 68 140 |
| 11 | 24 | 82 857 | 342 | 178 | non | non | 51 | 11 | 5 | 68 156 |
| 11 | 25 | 82 858 | 320 | 200 | non | non | 51 | 11 | 6 | 68 158 |
| 11 | 26 | 82 858 | 302 | 200 | non | non | 51 | 11 | 16 | 72 531 |
| 11 | 27 | 82 890 | 310 | 224 | non | non | 24 | 3 | 7 | 108 394 |
| 11 | 28 | 82 897 | 312 | 208 | non | non | 51 | 11 | 7 | 68 201 |
| 11 | 29 | 87 243 | 240 | 280 | non | non | 51 | 11 | 30 | 87 681 |
| 11 | 30 | 87 681 | 240 | 280 | non | non | 51 | 11 | 29 | 87 243 |
| 11 | 31 | 93 902 | 208 | 234 | non | oui | 5 | 2 | 9 | 132 684 |
| 11 | 32 | 101 843 | 264 | 256 | non | oui | 5 | 2 | 34 | 203 840 |
| 11 | 33 | 101 914 | 272 | 264 | non | oui | 28 | 27 | 30 | 164 437 |
| 11 | 34 | 105 408 | 328 | 320 | non | oui | 17 | 10 | 40 | 177 351 |
| 11 | 35 | 105 488 | 328 | 320 | non | oui | 17 | 10 | 42 | 177 386 |
| 11 | 36 | 105 566 | 286 | 312 | non | oui | 5 | 2 | 20 | 167 483 |
| 11 | 37 | 164 766 | 264 | 256 | non | non | 10 | 10 | 2 | 68 924 |

Toutes les solutions à partir du départ 18
| start 18 - # Solutions 14 ==== 128 139 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 18 | 1 | 52 662 | 272 | 168 | non | non | 5 | 2 | 19 | 167 247 |
| 18 | 2 | 52 667 | 192 | 248 | non | non | 40 | 2 | 25 | 181 574 |
| 18 | 3 | 52 744 | 262 | 224 | non | non | 17 | 10 | 15 | 156 272 |
| 18 | 4 | 53 153 | 190 | 256 | non | non | 39 | 3 | 60 | 279 777 |
| 18 | 5 | 53 375 | 296 | 168 | non | non | 19 | 19 | 24 | 211 340 |
| 18 | 6 | 54 058 | 208 | 232 | non | non | 5 | 2 | 18 | 166 281 |
| 18 | 7 | 54 080 | 176 | 248 | non | non | 37 | 19 | 27 | 239 076 |
| 18 | 8 | 57 385 | 192 | 328 | non | oui | 35 | 27 | 1 | 2 088 |
| 18 | 9 | 57 410 | 200 | 320 | non | oui | 35 | 27 | 14 | 38 834 |
| 18 | 10 | 57 509 | 190 | 330 | non | oui | 35 | 27 | 15 | 38 931 |
| 18 | 11 | 57 704 | 190 | 330 | non | oui | 35 | 27 | 16 | 39 117 |
| 18 | 12 | 58 199 | 184 | 336 | non | oui | 35 | 27 | 17 | 39 584 |
| 18 | 13 | 58 601 | 128 | 392 | non | oui | 35 | 27 | 3 | 2 351 |
| 18 | 14 | 114 610 | 176 | 232 | non | non | 26 | 19 | 28 | 239 077 |

Toutes les solutions à partir du départ 19
| start 19 - # Solutions 28 ==== 321 107 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 19 | 1 | 5 418 | 336 | 312 | non | oui | 9 | 9 | 2 | 57 015 |
| 19 | 2 | 5 448 | 336 | 312 | non | oui | 9 | 9 | 1 | 56 965 |
| 19 | 3 | 14 206 | 248 | 308 | non | oui | 13 | 10 | 18 | 156 283 |
| 19 | 4 | 14 484 | 296 | 284 | non | oui | 13 | 10 | 17 | 156 272 |
| 19 | 5 | 14 522 | 286 | 274 | non | oui | 13 | 10 | 16 | 156 272 |
| 19 | 6 | 14 540 | 286 | 274 | non | oui | 4 | 3 | 9 | 108 395 |
| 19 | 7 | 16 984 | 264 | 272 | non | oui | 36 | 27 | 29 | 164 435 |
| 19 | 8 | 18 402 | 232 | 304 | non | oui | 4 | 3 | 16 | 109 486 |
| 19 | 9 | 21 290 | 276 | 272 | non | oui | 4 | 3 | 20 | 110 622 |
| 19 | 10 | 21 563 | 286 | 304 | non | non | 32 | 3 | 43 | 136 421 |
| 19 | 11 | 21 563 | 286 | 290 | non | non | 32 | 3 | 48 | 136 546 |
| 19 | 12 | 21 992 | 296 | 304 | non | non | 32 | 3 | 44 | 136 421 |
| 19 | 13 | 21 992 | 296 | 290 | non | non | 32 | 3 | 49 | 136 546 |
| 19 | 14 | 22 007 | 310 | 234 | non | oui | 13 | 10 | 32 | 158 357 |
| 19 | 15 | 22 236 | 256 | 304 | non | non | 31 | 3 | 52 | 137 207 |
| 19 | 16 | 31 528 | 312 | 264 | non | non | 54 | 9 | 5 | 60 780 |
| 19 | 17 | 31 555 | 264 | 256 | non | oui | 34 | 19 | 25 | 211 544 |
| 19 | 18 | 31 731 | 310 | 234 | non | oui | 13 | 10 | 29 | 158 343 |
| 19 | 19 | 31 767 | 300 | 224 | non | oui | 13 | 10 | 28 | 158 343 |
| 19 | 20 | 31 767 | 264 | 256 | non | oui | 34 | 19 | 26 | 211 880 |
| 19 | 21 | 199 522 | 280 | 320 | non | non | 41 | 10 | 39 | 177 351 |
| 19 | 22 | 200 503 | 280 | 320 | non | non | 41 | 10 | 41 | 177 386 |
| 19 | 23 | 201 583 | 304 | 312 | non | non | 41 | 10 | 1 | 56 410 |
| 19 | 24 | 211 340 | 224 | 352 | non | non | 18 | 18 | 5 | 53 375 |
| 19 | 25 | 211 544 | 264 | 256 | non | oui | 29 | 19 | 17 | 31 555 |
| 19 | 26 | 211 880 | 264 | 256 | non | oui | 29 | 19 | 20 | 31 767 |
| 19 | 27 | 239 076 | 344 | 272 | non | non | 45 | 18 | 7 | 54 080 |
| 19 | 28 | 239 077 | 344 | 288 | non | non | 18 | 18 | 14 | 114 610 |

Toutes les solutions à partir du départ 27
| start 27 - # Solutions 30 ==== 198 763 Sec. ==== | ||||||||||
|
Start
|
Sol.
|
Time
|
DP
|
DS
|
SM
|
CT
|
End
|
Dual
|
Sol.
|
Time
|
| 27 | 1 | 2 088 | 192 | 328 | non | oui | 42 | 18 | 8 | 57 385 |
| 27 | 2 | 2 088 | 216 | 304 | non | non | 30 | 11 | 8 | 68 577 |
| 27 | 3 | 2 351 | 128 | 392 | non | oui | 42 | 18 | 13 | 58 601 |
| 27 | 4 | 13 338 | 248 | 224 | non | non | 24 | 3 | 11 | 108 845 |
| 27 | 5 | 13 655 | 272 | 232 | non | non | 39 | 3 | 45 | 136 423 |
| 27 | 6 | 13 655 | 202 | 248 | non | non | 40 | 2 | 23 | 181 453 |
| 27 | 7 | 13 655 | 192 | 248 | non | non | 40 | 2 | 26 | 181 575 |
| 27 | 8 | 13 655 | 284 | 252 | non | non | 39 | 3 | 47 | 136 472 |
| 27 | 9 | 13 761 | 262 | 224 | non | non | 24 | 3 | 8 | 108 394 |
| 27 | 10 | 20 511 | 272 | 246 | non | non | 39 | 3 | 46 | 136 423 |
| 27 | 11 | 20 511 | 202 | 262 | non | non | 40 | 2 | 24 | 181 453 |
| 27 | 12 | 20 511 | 192 | 262 | non | non | 40 | 2 | 27 | 181 575 |
| 27 | 13 | 20 605 | 248 | 274 | non | non | 24 | 3 | 19 | 110 621 |
| 27 | 14 | 38 834 | 200 | 320 | non | oui | 42 | 18 | 9 | 57 410 |
| 27 | 15 | 38 931 | 190 | 330 | non | oui | 42 | 18 | 10 | 57 509 |
| 27 | 16 | 39 117 | 190 | 330 | non | oui | 42 | 18 | 11 | 57 704 |
| 27 | 17 | 39 584 | 184 | 336 | non | oui | 42 | 18 | 12 | 58 199 |
| 27 | 18 | 39 993 | 176 | 292 | non | non | 58 | 2 | 36 | 605 912 |
| 27 | 19 | 91 999 | 256 | 264 | non | oui | 10 | 10 | 3 | 87 458 |
| 27 | 20 | 91 999 | 256 | 264 | non | oui | 10 | 10 | 4 | 87 458 |
| 27 | 21 | 92 030 | 256 | 264 | non | oui | 10 | 10 | 48 | 211 636 |
| 27 | 22 | 92 030 | 256 | 264 | non | oui | 10 | 10 | 49 | 211 636 |
| 27 | 23 | 124 318 | 292 | 228 | non | oui | 10 | 10 | 5 | 87 533 |
| 27 | 24 | 124 318 | 292 | 228 | non | oui | 10 | 10 | 6 | 87 533 |
| 27 | 25 | 124 338 | 292 | 228 | non | oui | 10 | 10 | 50 | 211 717 |
| 27 | 26 | 124 338 | 292 | 228 | non | oui | 10 | 10 | 51 | 211 717 |
| 27 | 27 | 138 295 | 262 | 244 | non | non | 58 | 2 | 32 | 203 761 |
| 27 | 28 | 164 417 | 256 | 248 | non | oui | 33 | 11 | 21 | 80 276 |
| 27 | 29 | 164 435 | 256 | 248 | non | oui | 44 | 19 | 7 | 16 984 |
| 27 | 30 | 164 437 | 256 | 248 | non | oui | 33 | 11 | 33 | 101 914 |
