Some programs available on this site propose several solutions to the traditional problem of the Euler's knight. This problem is tackled under two aspects.
- The algorithm
How to design the algorithm so that search is the fastest one ? How to take into account in the algorithm the constraints necessary to the development of a magic square and what are all the possible solutions ? These solutions are known as the 140 Euler's Magic Knight Tours (MKT). How to use the same algorithm to search knight's tours with different constraints (longest path without any crossing, path with imposed crossing points, close tours, 2kt tours, magic cube...)
- Data-processing technologies
How to simply integrate the search programm in a Web environment to make it directly usable through an HTML page or in an office document (Word, PowerPoint ...).
Thanks to several improvements in the algorithm and with the help of new processor power, the search's time has been divided by 40 in 13 years ! The 140 solutions are found in 0,7 day on an AMD Ryzen 5 1600X - 3.6GHz.
Algorithm is based on 64 interacting objects presented in this presentation 
. An ActiveX control can be integrated in a powerpoint. If you want to see it, you have to use "Regsvr32 Tool (regsvr32.exe)" to register Kmagic.ocx on your machine. Algorithm's statistics are provided through the mschrt20.ocx control. You have to download and register also this control.
The following table presents the results.
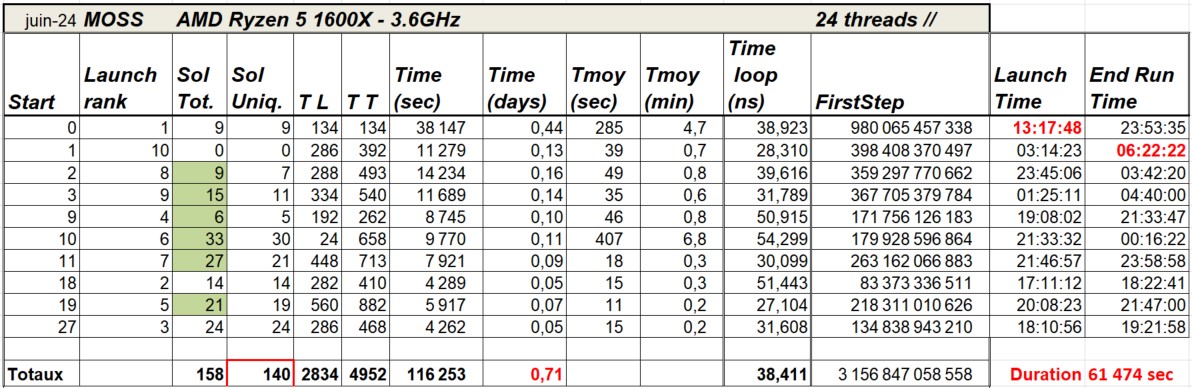
The meaning of the column are :
- Start : the number of th start square The squares of the chess-board are numbered from 0 to 63, from left to right and upwards. The starting zone includes squares 0,1,2,3,9,10,11,18,19,27
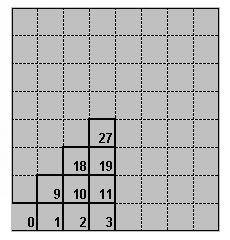
- rang : the order of each of the 10 runs. When a run is launched from a square, this one will be no more chosen as a possible end square, for the next runs from the other squares
- Sol. Tot. : number of solutions found for the run. Solutions can be linked by symetries as in this example
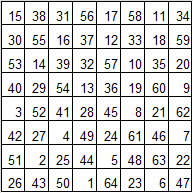
The reverse path of the first solution (each value x is replaced by 65 - x) provides the following figure.
This figure is symetric with the second solution.
- Sol. uniq. : number of solutions after all symetries have been eliminated
- Temps (sec) : time of run in seconds
- Temps (jours) : time of run in days (time in seconds/86400)
- Temps loop (ns) : time / Firstep in nanosecconds
- FirstStep : number of forward steps of the knight
There are 280 magic squares with different properties : standard magic tours, magic close tours, semi-magic tours where each quarter of the chessabord is itself a magic tour. Each tour is linked with its reverse magic tour. Therefore, there is ony 140 independant magic tours.
Close Tours
A close Tour (CT) is a tour where the start square and end square are linked by a knight step.
2KT Tours
Other types of tour could be searched on 8x8 board. For example, 2-kt tours that is, 1 to 32 and then 33 to 64 are at knight move but not 32 to 33 and the result is a special 2-kt magic tours. There are many more 2k-tours than classical magic tours.
With the same idea, 3-kt tour is a tour with 1 to 16, 17 to 48 and 49 to 64 are at knight move but not 16 to 17, 48 to 49 Similary, 4-kt tours is composed of 4 segments 1 to 16, 17 to 32, 33 to 48 and 49 to 64. The computed time to find all the solutions for these types of tour is very large. An estimation is in progress ...
TANGRAM
The same algorithm was used to count the number of possible placements of 11 geometric pieces in a hexagonal TANGRAM. Several adaptations had to be made.
Author : Yann DENEF mailto:ydenef@orange.fr