
2-kt magic tours on an 8x8 board
A 2-kt magic tour is a knight tour with moves 1 to 32 and then 33 to 64 are at knight move but not 32 to 33. These special tours have been searched on a 8x8 board. The same program, used to find magic tours on a 8x8 board was re-used with modifications.
These modifications have been made while retaining the same principles for the algorithm
The first attempt to find, on a 8x8 board, 2-kt tour provided 8437 solutions. The algorithm used to find classical magic tours was modified only to take into account the special knight move between 32 and 33. Each solution must have a « associated dual solution », eventually itself, that is the reverse path of the original solution. The association table using these 8437 solutions shows that some solutions are alone, without an associated dual solution
Therefore, some solutions are missing. So the modifiations of the basic algorithm are not right. The explanation is quite simple. The search is composed of 2 phases. The first phase from index 1 to 32 and the second phase from index 33 to 64. During the first phase, some rules used for the basic search don’t apply and must be replaced by others rules.
The board below assists in understanding 2 new rules that must be applied during the first phase

Look at square A1 with index 32. In a classical tour, the knight could not continue because square B3 and C2 are occupied with index 31 and 29. Algorithm has to be modified to authorize this situation
The square A8 with index 33 cannot be the end of path (odd index). However, this square has only 1 neighbour (B6). C7 is occuppied with index 14. With 2-kt search, square A8 wins a new neighbour if the index is 33. This is an other modification of the algorithm.
Another subtle modifiation must be added in the algorithm during the first phase.
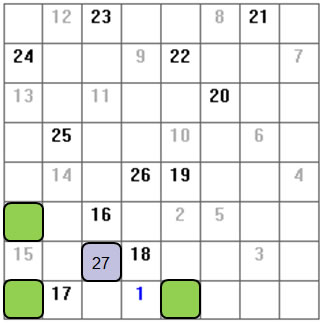
The knight at square C2 with index 27 can step forward on one square among A1, A3 or E1 (green squares). Each of these squares has only 1 other neighbour. For a classical Knight Tour, the knight must move back. For 2KT tour, the knight moves on one green square, the second green square is marked as the end (index 64) and the third green square is marked as the end of the first phase (index 32). From index 32, the knight can escape elsewhere to many other squares. Each of the 3 green squares can take one of the 3 roles. So, passage between phase 1 (index 1 to 32) and phase 2 (index 33 to 64) must be precisely controled.
After these corrections, 11194 solutions are found. Each solution has a dual solution associated with it ; may be the set of every solutions are found.