
2KT tours on a 8x8 chessboard
The first chart below shows the repartition of the 11194 solutions depending on the start square. For each start, it shows also the time spent to find them and the properties of the solutions :
1) Idem Moves : move between 32 and 33 is the same as move between 1 and 64 2) Auto shift32 : shift 32 on every indexes provides an identical chessboard 3) Close Tour : knight move between index 1 and index 64 4) Auto Dual : direct and reverse path are identical 5) Full Magic : tour is magic in the diagonal as well 6) 1/4 Magic : each quarter of chessboard is magic (sum of 130)There are 5194 "auto dual" solutions and 6000 other solutions (3000 direct + 3000 reverse). The number of unique solutions is 3000 + 5194 = 8194.
The raw result from the 10 starts are merged into this file. For each start in the set 0 (A1), 1 (B1) , 2 (C1), 3 (D1), 9 (B2), 10 (C2), 11 (D2), 18 (C3), 19 (D3), 27 (E4) there are 25 files :

The second chart focuses on the total number of solutions (sum of the solutions from the 10 start squares). These solutions are sorted according to their specific move between 32,33 (column "All Moves"). The first column shows all solutions. The other columns ("Idem Moves","Auto Shift32","Close Tours","Auto Dual","Full Magic","1/4 Magic") shows the number of solutions for a specific property.

The reverse path of this solution provides another solution belongs usually to another equivalence class. The main representative of the reverse solution is the called the dual solution. (look at the exemple). Sometimes, source (main representative) and reverse solution belong to the same equivalence as the exemple of start D1 - rank 2. Source and dual solution belong to the same equivalene class : the solution is auto-dual
The raw results has been used to build the correlation table (each solution is linked with its dual solution). This information, provided by a specific program, is presented in an ascii format and Excel format. For each case, properties of move 32-33 and move 1-64 were added.
Some tours among these solutions are a subset of Empress Tours (mayhematics.com) described by George Jellis.With the specific move 32-33, there is a new property called CT. There are 2 types of CT : "Close tour" with 1 specific move between 32-33 and a knight move between 1-64 (182 solutions) or "Idem" with 2 identical moves between 32-33 and 1-64 (3230 solutions). By design of the algorithm, move between 32-33 is never a knight move. In addition, with Idem property, these 2 moves are identical. By shifting index along the way, one can find in most cases other magic tours for one or many shift values. It's not the case for a small number of solutions as mentioned below.
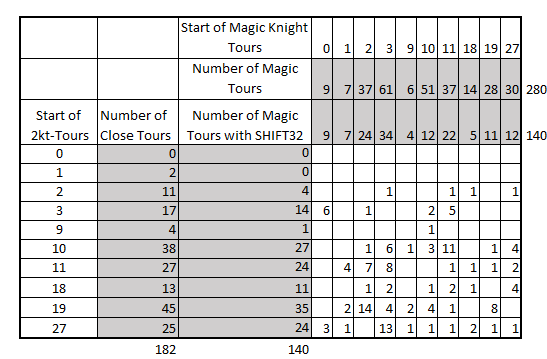
When type of CT is "Close Tour" and shift value is 32, one can also build a "shif32 chessboard". The only move that is not a knight move becomes the move between 1 and 64. Therefore, if this chessboard is Magic, it must be already known : it's a standard Magic Tour. In this case, the button "Shift 32 Solution" provides a link to this classical Magic Tour. There are 182 2kt tours with the property "Close Tour". Among these 182 tours, 140 provide a Magic tour after the shift32 operation.
The number of associations between magic squares and 2-kt magic squares, after a shift of the index of each cell by 32, is sorted in the table below based on their starting cell.
Moreover, the ASCII formats (output of fprintf) are transformed in order to produce images in "png" format.