When a magic knight tour is found, the opposite way having for origin the last square of the found way gives also a magic square. By testing the 10 independent start squares of the starting zone ,each solution is found twice.

It is possible to reduce the total search time (all magic squares starting from all the possible origins of the starting zone). During the research, it often happens that the last square (if the way is possible) is known by advance. Indeed, when knight arrives on a square which hase only two neighbors A and B and of which each one of these two neighbors has only one another neighbor (except the current box), it is necessary to be able to continue the way, to go either towards A and so B is the end of the course, or or towards B and so A is the end of the course. If the end is already fixed, one can go neither towards A, nor towards B and it is thus necessary to move back.

When all the ways are found starting from a given start square X, one can in other research having for origin another square, prohibit X as a possible last square. Thus, the tree of research is smaller.

The next 10x10 table indicates in line and column the 10 start squares from which it's possible to obtain all the solutions. For each start square, the number of solutions for a given last square is indicated. A solution can be found either by the direct way, or by using the opposite way.

The principle of research optimized is as follows: one seeks all the solutions starting from the first start S1. One seeks then all the solutions starting from the S2 start square by prohibiting the solutions which provide S1 as last square. Then one seeks the solutions starting from the third S3 start, by leaving the arrivals giving S1 and S2… and so until the tenth departure.

It is not obvious to find the order in which various research must be carried out to minimize total time. On the following figure, the order of the departures is indicated. It's not sure this order is the best, i.e. that which produces a minimum search time. There is in theory 10! possible combinations. In our choice, the first research is carried out starting from box 0, i.e. a corner of the chess-board. Thus, in following research, all the solutions leading to a corner will dropped. The second research is carried out from square18 (C3 on a chessboard). The continuation consists of the squares 27 then 9 then 19 then 10 then 11 then 2, 3 and finally 1.

The following figure is read thus. Each line represents a start square. The sum of the numbers on each line (or column) indicates the number of magic squares obtained starting from this departure. There are 280 of them. The boxes of possible arrivals are presented in column. When a number is present in a box, it indicates the number of solutions for a given departure, indicated by the number of line and for a given arrival - brought back in the starting zone - indicated by the number of column. A number on green bottom indicates a solution found in the direct way and a number on purple bottom indicates a solution which was previuosly found on another direct way. So algorithm take into account this information and theses solutions are not serached again..

All the ways having their arrival on the same square as the departure (after rotation and symmetry of course) are directly obtained. (squares on diagonal)

Researchs ran first on pentium 4, 2,4 Ghz and after on pentium 4 1,7 Ghz. Times are expressed in seconds. Line "# Solutions" indicates, for each start square the number of solutions found by using this optimized algorithm followed by the number of solutions obtained with the initial algotithm (without this optimization, neither solutions are dropped). The search times, obtained by the initial algorithm are indicated in order to compare the benefit. One sees that the larger the order of research is, the more the profit is significant.

The first research is carried out starting from box 0, i.e. an angle of the chess-board. It lasts nearly 10 days. One could plan to finish research by this departure. However, while starting with this square, all following research starting from the 9 other departures are much less long because one prohibits the ways then being able to lead in a corner of the chess-board. This occurs as soon as the knight arrives at a jump of a corner, without continuing by this corner.

However, it is probable that this order of research can be optimized in order to have, a total time lower than 26 days. Moreover, improvements on coding the algorithm are surely possible.

The algorithm run on a pentium 4 - 2,4 Ghz finds 158 solutions in 26,4 days. There is more than the 140 awaited solutions because the ways having the departure on arrival on the same box (with rotations and symmetries near) are always counted twice. There are 36 solutions in this case. These 36 solutions constitute only 18 independent solutions.

The corrected number is thus 158 - 18. The 140 independent solutions well are found.

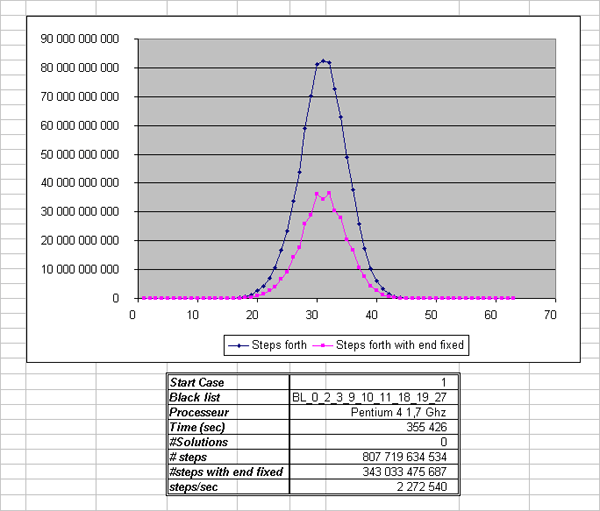
The number of steps forth and the number of steps forth with end fixed, for a given index is provided on the following figure for the start case 1. All te curves for the 10 start cases are very similar.

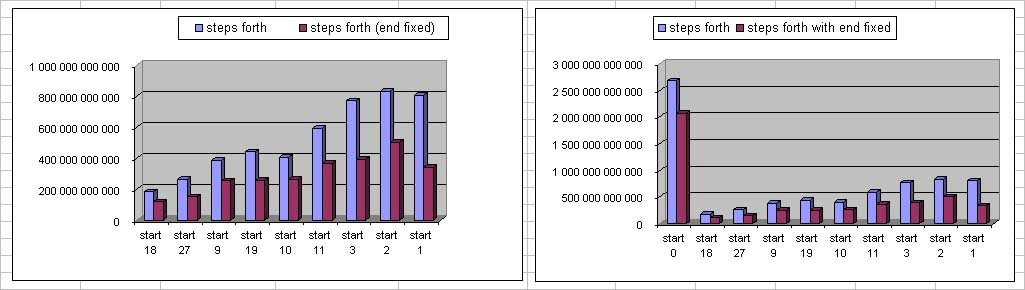
The total numbers of steps forth (in blue) and steps forth with end fixed (in red) for the 10 starts {0,18,27,9,19,10,11,2,3,1} is presented on the last diagram.

The order of presentation is the order of start square's trial.